The 20th century witnessed major breakthroughs in standard cosmology, bringing us face-to-face with one of life’s most profound mysteries: how and why did the universe come into being? For a while, naturalistic explanations for the universe’s origin felt puzzling and even counterintuitive. In contrast, the idea of a creator God—a transcendent and foundational consciousness—seemed to fit the attributes of the first cause.
(*The following is an excerpt from “Does the Universe Paint God Out of the Picture?” by Luke Baxendale. This is part three of four in the book. It may be helpful to read part two first.)
But then the picture began to shift. Enter the realm of quantum cosmology, a daring and cutting-edge field born from the union of quantum mechanics and general relativity. Many naturalists now look to quantum cosmology, hoping its breakthroughs will finally offer a naturalistic explanation for the universe’s existence. Suddenly, the idea that the universe could create itself seemed possible, suggesting that the existence of God was no longer a necessary explanation.
Could quantum cosmology finally crack the code of how, and why, the universe began? Does it provide more persuasive, naturalistic explanations for why the universe exists?
Stephen Hawking believed so.
Now be prepared: quantum cosmology is a confusing and challenging field, known for its perplexing concepts and intricate theories that may seem baffling or even counterintuitive at times. Don’t be disheartened if certain aspects seem challenging to understand; after all, no one truly understands it in its entirety. The confusing nature of quantum cosmology is what makes it so interesting.
Stephen Hawking and Quantum Cosmology
Stephen Hawking, an English theoretical physicist and cosmologist, was an extraordinary individual who defied the odds. Despite battling a rare early-onset, slow-progressing form of motor neurone disease that gradually paralysed him over decades, Hawking emerged as one of history’s most influential theoretical physicists. A mathematical prodigy, his groundbreaking work on the origin and structure of the universe, spanning the Big Bang to black holes, revolutionised the field.
Although Hawking had played a crucial role in proving the singularity theorems, working with Roger Penrose on their landmark 1970 result and later co-authoring the foundational 1973 monograph “The Large Scale Structure of Space-Time” with George Ellis, he found their implications of a beginning philosophically unsettling. The theorems showed that under general relativity, the universe emerged from a singularity, a point of infinite density where physics breaks down. What troubled Hawking was that if the universe began at a singular point where physics itself broke down, how could science ever hope to explain the ultimate origin of everything? A beginning of this kind seemed to place the universe’s creation beyond the reach of the usual reductionist tools of modern scientific inquiry. As a result, Hawking began to formulate a cosmological model that he hoped would eliminate this troublesome initial boundary condition.
So, in 1981, Hawking gathered with some of the world’s leading cosmologists at the Pontifical Academy of Sciences, a vestige of the coupled lineages of science and theology located in a grand villa in the gardens of the Vatican. There, Hawking presented a revolutionary idea: a self-contained universe, with no definitive beginning or end.
But how can a universe emerge and still have no clear beginning? Hawking proposed that near what might be considered the beginning of the universe, time behaves like a spatial dimension, resulting in a universe that is self-contained and without a boundary. This implies that there is no distinct point at which the universe began; instead, it simply “is” in a manner that does not require an external cause or a specific moment of creation.
Hawking’s bold proposal hinged on the application of quantum mechanics, the physics of the infinitesimally small, to analyse the universe at its nascent stage. In doing so, he contested the traditional notion of a ‘definite beginning’ and presented a formidable challenge to the foundation of the Kalam cosmological argument.
Quantum mechanics (which I’ll refer to as QM) is the study of how the world operates at very small scales, where things can become quite strange. QM describes the interactions and motions of subatomic particles that exhibit both wave-like and particle-like behaviour. While the universe today is vast and expansive, at some point in the finite past, the universe would have been so small that physicists would need to consider how quantum mechanical effects would influence gravity. It is thought that in such a small space, Einstein’s theory of gravity (general relativity) would no longer be applicable.
Many physicists have proposed that gravitational attraction would have functioned differently in the early universe, as it would have been subject to quantum mechanical principles and unpredictable quantum fluctuations. Although no adequate theory of “quantum gravity” that coherently synthesises general relativity with QM has been formulated yet, Hawking applied QM ideas about how gravity might operate on a subatomic scale to describe the universe in its earliest state. In collaboration with James Hartle, Hawking developed a quantum cosmological model based on the Wheeler-DeWitt equation. They called this their “no-boundary proposal,” which was fully formulated in a 1983 paper.[i]
Hawking and Hartle’s quantum cosmology applies QM to understand the physics of the early universe, employing the concept of wave-particle duality. But what exactly is this strange phenomenon, and how did we even discover it?
The concept of wave-particle duality is not well understood. The story starts with a mystery that took over a century to unfold. Back in 1801, Thomas Young set up what became known as the “double slit” experiment. He shone light through two narrow slits and watched it create rippling interference patterns on a screen, clear proof that light behaves like a wave. Then in 1905, Einsteins work on the photoelectric effect revealed that light also comes in discrete little packets of energy called photons. So, which is it: wave or particle? Surely light can’t be both?
The 1920s then brought even stranger revelations. Scientists discovered that electrons, atoms, and other subatomic particles also show this dual nature. But here’s where it gets really weird: these particles aren’t simply “switching” between being waves or particles. Instead, this suggested something more fundamental about quantum systems, that we observe about their nature depends on how we choose to measure them.
Physicists in the 1920s and 1930s sought to explain or at least accurately describe these strange results. Erwin Schrödinger developed a mathematical framework to characterise wave-particle duality, enabling physicists to predict or calculate the probability of a subatomic particle being found in a specific location upon detection. Think of it as describing a ghostly cloud of possibilities that exists until the moment we measure it. The wave function captures these possibilities and “collapses” when the photon, as a wave, encounters an observer or detector and the “probability wave” collapses.
The wave function also describes “superposition,” but this doesn’t mean the particle is literally “in multiple places at once” in any classical sense. Rather, it means the system genuinely lacks definite properties until measured. Quantum systems can exist in combinations of different possible states simultaneously. When a measurement occurs, we observe definite outcomes, and the wave function appears to “collapse” to reflect this new information. However, whether this collapse represents a physical process or simply an update of our knowledge is debated (I lean toward the latter).
It’s also important to clarify that the term “observed” in this context does not necessarily imply that a conscious observer is needed for the wave function to collapse. The “collapse” can also occur through interaction with the environment, as described by decoherence theory, which explains how quantum systems lose their coherent superposition properties through unavoidable interactions with their environment. This aspect of QM is still debated and open to interpretation.
Admittedly, it’s all rather perplexing. The notion that a subatomic particle exists without a definite character, represented as a mathematical probability until it interacts or is observed, challenges both physicists and common sense alike. Indeed, the physics of the very small has proven to be the physics of the utterly bizarre. I suspect that much of this “weirdness” arises from our tendency to impose classical mental pictures on quantum phenomena. Our everyday intuitions about reality are, in many cases, simply the wrong tools for understanding the quantum world.
So, how does this connect to cosmology? In the first fractions of a second after the Big Bang, the universe would have been so small that QM would have been crucial for understanding how gravity functioned. To understand how gravity would have operated in such a confined space during the very earliest stage of the universe, scientists have crafted an equation that fuses mathematical concepts from QM and general relativity. This equation is known as the Wheeler-DeWitt equation, named after its developers, John Wheeler and Bryce DeWitt. Many physicists consider this equation to be, at the very least, an initial step towards the development of a quantum theory of gravity. It represents an effort to unify general relativity and QM within an approach known as “quantum geometrodynamics.” It’s an equation that describes the quantum state of the universe without any explicit time dependence. This absence of time is a peculiar feature that gives rise to what physicists call the “problem of time” in quantum gravity.
Let’s pause for a moment to recap so things stay clear. In standard QM, various solutions to the Schrödinger equation enable physicists to create a mathematical expression known as a wave function. This wave function, in turn, allows them to calculate the probability of obtaining specific measurement outcomes, such as finding a particle at a given position or with a given momentum. The wave function describes the range of possible outcomes and their probabilities; it does not reveal the properties of the system before measurement, but rather prescribes what can be expected if a measurement is made.
In quantum cosmology, however, the focus shifts to the universe as a whole, and this is where the Wheeler-DeWitt equation comes in. Solving this equation enables physicists to formulate a wave function for the entire universe. The Wheeler-DeWitt equation is conceptually similar to the Schrödinger equation in that it involves a wave function. However, while the Schrödinger equation’s wave function describes the quantum states of particles or fields, the wave function in the Wheeler-DeWitt equation describes quantum states of the entire universe. It describes a range of potential universes, each with distinct gravitational fields, which can be understood as different curvatures of space and unique mass-energy configurations. In other words, the universal wave function, derived from the Wheeler-DeWitt equation, outlines the various spatial geometries and matter configurations that a universe could assume, revealing the probability of a universe emerging with specific gravitational and mass properties.
By solving the Wheeler-DeWitt equation, physicists can determine the wave function for the entire universe and subsequently calculate the probability of a given universe with a particular gravitational field and a distinct curvature mass-energy pairing coming into existence.
So, to understand how quantum cosmology could be used as a theory that explains the existence of the universe, it’s crucial to focus on three key elements:
- The existence of our universe with its unique attributes—the phenomenon that needs to be explained.
- The universal wave function—the mathematical construct that provides the explanation.
- The Wheeler-DeWitt equation and the mathematical process for solving it—the justification for using the universal wave function as an explanation for the universe.
Stephen Hawking developed a quantum cosmological model based on the Wheeler-DeWitt equation to describe the universe as a consequence of a theory of quantum cosmology. His primary goal was to determine the wave function of the entire universe, a mathematical expression that encapsulates all possible states of the universe. By solving the Wheeler-DeWitt equation with a specific “no-boundary” condition, they calculated the relative probabilities of different universes emerging, including one like ours with its specific gravitational field and physical properties. If the probability for our universe is non-zero, Hawking argued this could provide a fundamental explanation for the universe’s existence grounded in the laws of quantum physics
Together, Hartle and Hawking developed a formula that described a universe without a clear beginning, the so-called “wave function of the universe,” which encompasses the entire spacetime in a timeless quantum description. Their approach to the Wheeler-DeWitt equation suggested that space and time could emerge smoothly from a quantum state—specifically through a path integral over compact, boundaryless Euclidean geometries—bypassing the need for a singularity like in the traditional Big Bang model. This concept challenges notions of creation and, consequently, the idea of a creator. In essence, they found a solution to the Wheeler-DeWitt equation that yields a universal wave function describing a self-contained universe like ours.
However, there were a few complications along the way…
The Limitations of Imaginary Time in Explaining the Universe
Hawking realised that accurately calculating the early universe’s likely state was intractable within the framework of real time. To make the problem tractable, he reframed the calculation in “imaginary time.”
Think of real time as an arrow running past → present → future. Imaginary time sits at right angles to that arrow in the complex plane, like adding a second direction for time in the maths. In this picture, histories can be smoothed out, and the equations avoid the abrupt “beginning” that causes trouble in real-time formulations. Here’s a diagram to visualise the idea:
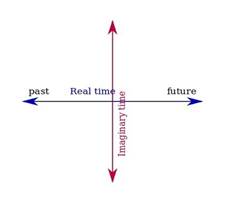
What is imaginary time, exactly? Imagine taking our familiar concept of time and multiplying it by “i”, which is the mathematical symbol for the square root of negative one. This might sound absurd (how can time be imaginary?), but this mathematical sleight of hand transforms Einstein’s description of spacetime in a profound way.
Normally, Einstein’s spacetime has what physicists call a “Lorentzian signature”, which is just a fancy way of saying that time behaves fundamentally differently from the three dimensions of space. But when we switch to imaginary time, spacetime becomes “Euclidean”, meaning time starts behaving just like another spatial dimension.
Why does this matter? When physicists try to calculate what happened during the universe’s birth, the mathematics becomes incredibly complex and often breaks down. But in imaginary time, these same calculations become much more manageable.
This replacement, called a Wick rotation, is a 90° turn of the time axis in the complex plane. It’s a mathematical device, not a claim that we literally experience a second kind of time. After the Wick rotation, time acts like a spatial dimension, so the resulting geometry can be finite yet without a boundary, i.e. no singular first instant.
This reimagining led to Hawking’s famous “no boundary” proposal. This model avoided a cosmological singularity (a beginning in time), while still preserving a finite past. He envisioned the early universe as having a rounded geometry, much like the curved surface of the Earth. In this analogy, the South Pole represents the “beginning” of the universe, and the circles of latitude represent the passage of time. Just as it is meaningless to ask what lies south of the South Pole, it becomes nonsensical to ask what occurred “before” the rounded-off section of spacetime in Hawking’s model. This model implies no need for a beginning as such, yet the past remains finite.
In ‘A Brief History of Time,’ Hawking presented this result as a challenge to the idea that the universe had a definite beginning in time. He argued that this mathematical model suggested the universe would not need a transcendent creator to explain its existence. After he explained how this “calculational aid” eliminated the singularity, he famously observed: “So long as the universe had a beginning, we would suppose it had a creator. But if the universe is really completely self-contained, having no boundary or edge, it would have neither beginning nor end; it would simply be. What place, then, for a creator?”[ii]
Hawking’s proposal sparked widespread belief that he had dismantled the Kalam cosmological argument for God’s existence, particularly its claim that “the universe began to exist.” By the 1990s, Hawking single-handedly began to shift perceptions about the Big Bang Theory’s implications.
Nevertheless, Hawking’s approach relied on a clever but controversial mathematical move: replacing real time with “imaginary time.” While this substitution made the equations work beautifully, it lacked any physical justification beyond mathematical convenience. The crux of the problem wasn’t Hawking’s mathematics; it was his interpretation of what those equations meant. Imaginary time is purely a computational tool that bears no resemblance to anything we observe in the physical universe. When time is confined to the imaginary axis of the complex plane, it loses physical meaning and becomes conceptually unintelligible as a description of our reality. Hawking himself acknowledged this limitation, recognising that his approach had instrumental rather than realistic value. Yet he often spoke of his mathematical expressions as if they carried genuine physical significance, despite incorporating a fundamentally unphysical concept. Our understanding of time is rooted entirely in real, observable experience, and so it is difficult to interpret what the use of imaginary time implies within the context of our universe’s actual spacetime geometry.
Hawking was aware of these issues, and in his Brief History, he candidly described his use of imaginary time as a “mathematical device (or trick).” He acknowledged that once his mathematical depiction of the geometry of space is transformed back into the real domain with a real-time variable, the domain of mathematics that applies to our universe, the singularity reappears. In his own words: “When one goes back to the real time in which we live, however, there will still appear to be singularities… Only if we lived in imaginary time would we encounter no singularities… In real time, the universe has a beginning and an end at singularities that form a boundary to spacetime and at which the laws of science break down.”[iii]
Questioning the Absence of a Singularity in Hawking and Hartle’s Universe Model
Another thorny issue emerges in the Hartle-Hawking model when you dig into their use of the path-integral method, a tool pioneered by Feynman. This method is widely used in QM to sum up mathematical expressions describing the potential paths of quantum particles, like electrons or photons.
To grasp what’s happening here, think of it this way: suppose you’re trying to get from your house to the local shops. Common sense says you’d take the most direct route. But in the quantum world, particles don’t behave with such pedestrian logic. An electron “traveling” from point A to point B doesn’t simply choose the shortest path. Instead, it somehow samples every conceivable route: the direct line, certainly, but also wild detours that spiral outward, loop back, or take seemingly absurd scenic routes. The path integral method determines the probability of a particle’s movement by considering the contributions of all these paths, leading to the particle’s final behaviour as a combination of all possible paths.
When applying this concept to the universe’s history, Hawking and Hartle adapted the path-integral approach to account for all conceivable historical trajectories or ‘paths’ that the universe might have taken. This led them to propose a finite but boundaryless universe, utilising complex (imaginary) time paths, which contrasts with the singular origin suggested by classical Big Bang Theory. In their model, they construct a ‘universal wave function’ within ‘superspace’, a conceptual framework representing all possible geometries and matter configurations of the universe. This includes calculating the probabilities of various universe configurations, thereby including the likelihood of universes like ours emerging.
But here’s where the model blinks. To even start applying the path-integral method to the universe, you still need some form of pre-existing reality, such as physical laws, a quantum vacuum, or another fundamental structure. To apply the path-integral method, or any quantum mechanical approach, to the entire universe, there must already be a general concept of what constitutes the “universe.” This implies a need for some form of pre-existing structure or framework within which the mathematics can be applied. This reliance on pre-existing conditions means that the model does not really resolve the question of how or why the universe exists in the first place.
Although the “no-boundary” model replaces the classical Big Bang singularity with a quantum framework, the model itself depends on a specific set of initial conditions and physical laws that must already be in place for the universe to evolve as described. For instance, it presupposes boundary conditions such as Ψ = 1 at vanishing spatial volume (a → 0) and assumes the prior existence of quantum mechanical principles, including path integrals, configuration spaces, and wave function dynamics. These prerequisites aren’t explained, just asserted; they become the de facto “creation” point, as they establish the immutable rules governing how spacetime emerges from the quantum vacuum.
While the proposal smooths out the infinite density of a physical singularity by introducing a four-dimensional geometry in imaginary time, this merely replaces a temporal starting point with a conceptual one. The quantum formalism itself becomes a kind of non-physical starting point, requiring an irreducible mathematical foundation, such as superspace, quantum gravity axioms and boundary rules. That’s fine, but Hawking’s claim to have eliminated a temporal beginning depends on how he chooses to interpret his model’s multi-step formalism after the fact, rather than actually eliminating the causal prerequisites altogether. This approach shifts rather than resolves the problem of origins: the proposed quantum emergence still relies on a structured, preconfigured framework that raises similar metaphysical questions about why these specific quantum preconditions exist in the first place.
So, while the mathematical framework would appear to avoid physical singularities, it does not remove the need to explain why these particular quantum preconditions are there at all. Hawking’s dismissal of a temporal beginning occurs only at a later stage in this multi-step calculation process, leaving the question of ultimate origins unresolved.
I won’t press this point too strongly, as there are bigger issues to consider. If you’re well-versed in quantum cosmology, you can decide for yourself if this reasoning holds water. This argument rarely sparks the same controversy as debates over imaginary time. Still, there’s an interesting tension here: while the Hartle-Hawking model offers a valuable perspective in quantum cosmology, its reliance on a pre-existing notion of the universe (however vaguely defined) and the conceptual leap involved in using imaginary time raise significant questions about whether this model really explains the existence of our universe from nothing.
Constraints on Mathematical Freedom: The Role of Information in Quantum Cosmological Models
The Hartle–Hawking model, for all its elegance, runs into another revealing problem: it needs constraints. This isn’t just a technical detail; it cuts to the heart of what we mean by “explaining” the universe.
Here’s the crux: To solve the Wheeler–DeWitt equation and get a “wave function of the universe,” scientists must sift through a mind-boggling number of possibilities and narrow them down to a smaller, more manageable selection for analysis. Hartle and Hawking used a clever shortcut, the “path integral” approach (which sums over all possible spacetime geometries), but in practice, they focused on universes like ours with specific properties: isotropic (uniform in every direction), closed (self-contained and curved), spatially homogeneous (uniform in composition), and possessing a positive cosmological constant.
This naturally helped narrow the infinite possibilities to a manageable few, making calculations possible. But it also raises an awkward question: are we really discovering what the maths predicts, or just getting back what our assumptions smuggle in? Such filters do not merely describe; they prescribe, and where prescription is doing the heavy lifting, the explanans already embodies the target pattern.
To tackle the inherent complexity of these problems, Hawking and Hartle developed the ‘mini-superspace’ approximation, a technique that restricts analysis to a limited set of spatial geometries rather than wrestling with all possible configurations. This approach allows researchers to focus on specific gravitational field scenarios and explore how universes like our own might emerge as viable solutions.
However, this makes you wonder. The Wheeler-DeWitt equation naturally allows for infinite possible solutions, but arriving at a unique universal wave function requires carefully chosen boundary conditions from the outset. As Alexander Vilenkin points out, these boundary conditions are mathematically necessary to constrain the equation’s solutions. Yet by imposing such restrictions and cutting down the “degrees of freedom”, physicists inadvertently introduce additional information into their models, the very information they’re attempting to derive from first principles. Vilenkin notes:
“In ordinary quantum mechanics, the boundary conditions for the wave function are determined by the physical setup external to the system under consideration. In quantum cosmology, there is nothing external to the universe, and a boundary condition should be added to the Wheeler-DeWitt equation.”[iv]
The need to limit the almost infinite mathematical possibilities of the Wheeler–DeWitt equation in order to reach the right solution suggests that the universal wave function, which supposedly explains the existence of our universe, does not emerge naturally from the mathematics itself, but rather from the boundary conditions and restrictions that theorists impose on its potential solutions.
Physicists are relying on empirical knowledge of our universe (the “outcome”), rather than any physical theory that can independently justify the precise restrictions Hawking and Hartle impose on ‘superspace.’ In theoretical physics, ‘superspace’ refers to the set of all possible spatial geometries and gravitational field configurations. For a quantum cosmological model to realistically explain the existence of our universe, naturalistic physicists ought to provide a solid, non-circular physical reasoning for the specific constraints they apply.
James Hartle himself acknowledged this limitation, stating,
“Every time when we do one of those calculations, we have to use very simple models in which lots of degrees of freedom are just eliminated. It’s called mini-superspace… it’s how we make our daily bread, so to speak.”[v]
Daily bread or not, Hawking and Hartle’s assumptions about the universe were modelled based on the properties of our own universe. The model depends on information introduced from outside the formalism, an imposed specification. By narrowing the scope of superspace to universes like ours, they risked circular reasoning, essentially building the answer into their initial assumptions. The issue is that the moment you select one option over countless others, you are inevitably introducing extra information into the system. In quantum cosmology, specifically in relation to the Wheeler-DeWitt equation, the choice to exclude nearly an infinite number of potential mathematical solutions, whether through directly imposed boundary conditions, limiting the possible universes under consideration, or both, amounts to a significant injection of information into the mathematical frameworks used to model and explain the existence of the universe. This infusion of extra information lies at the heart of the debate.
Philosopher Stephen C. Meyer has advanced this argument, emphasising that the selection of these constraints is not determined by the Wheeler-DeWitt equation, a deeper theorem of gravity, or other fundamental physical theories. Rather, these decisions rest solely in the hands of the theoretical physicist, an intelligent agent acting with a specific goal.
Meyer goes on to suggest that intelligence—understood as having foresight, selection ability, and the capacity to aim at particular outcomes—may have played a role in shaping the cosmos. Intelligent agents introduce targeted information to realise specific ends. A computer program, for instance, does not emerge spontaneously from circuitry or the physical laws underlying it; it arises from a programmer’s directives. Similarly, every quantum cosmological model that attempts to explain our universe’s existence requires scientists to strategically limit an almost infinite number mathematical possibilities, effectively injecting targeted information to guide equations toward a particular result: a cosmos that looks like this one.
But where does this crucial information originate? It’s not enough to ask about the source of matter, energy, or space-time. We must also wonder about the origin of the very information needed to make existence-describing equations work. Can physical laws alone account for this?
In theory that’s unlikely. In this light, the link between quantum cosmology and the role of intelligence in the universe’s origin becomes easier to see. These theories depend on highly specific initial conditions, requiring carefully chosen and information-rich foundations. The degree of specificity demanded in these models mirrors patterns we usually associate with purposeful design, suggesting that mind—not just matter—may have been an ingredient in bringing about the ultimate event. This is not an argument from ignorance but rather a recognition of the indispensable role of information, foresight, and precision—traits we routinely observe in intelligent agency. As Stephen Hawking once mused, something (or dare I say someone) must “fire into the equations” the specificity and information needed to bring the universe into existence. This concept echoes the biblical notion that “in the beginning was the Word,” implying an origin rich in intent and meaning.
Now, I’m not saying this makes a case closed. It’s just a musing, an invitation. Quantum cosmology, at the very least, nudges us to rethink the origin story by foregrounding the role of intelligence to provide the necessary information and directed choices, which challenges the notion that the universe can be fully explained through “blind” and unguided natural processes. And if you look at it that way, Hawking’s claim to have done away with the idea of ultimate intelligence seems, well, a little too quick on the trigger.
Vilenkin’s Quantum Tunnelling Proposal
At a similar time when Hawking and Hartle published their work on quantum cosmology, Alexander Vilenkin put forward a bold alternative: the universe could have “tunnelled” into existence. His idea, based on “tunnelling wave functions”, sits alongside the Hartle–Hawking no-boundary proposal as one of the field’s most popular models. For some, quantum tunnelling offers a quasi-mechanistic way to explain why there is a universe at all.
First, a quick take on quantum tunnelling. In classical physics, objects are bound by strict energy constraints. Imagine a ball rolling toward a hill: if it doesn’t have enough energy to climb over, it will stop or roll back. However, in the quantum realm, particles behave more like waves than solid objects. Thanks to their wave-like nature and the inherent uncertainties of quantum mechanics, there’s a small but real probability that a particle can “tunnel” through an energy barrier and appear on the other side, even if it doesn’t have enough energy to cross it in classical terms.
Vilenkin scales this up to the cosmos. In his model, you assign a wave function to the universe and study it with the Wheeler–DeWitt equation (a quantum-gravity analogue of Schrödinger’s equation). In a simplified “minisuperspace” description, the cosmos is summarised by its overall size. There’s a potential barrier between a state with zero size and a tiny, closed universe. The “from nothing” claim is technical: “nothing” is not empty space; it’s the absence of classical spacetime altogether. In this timeless framework, tunnelling means the universe’s wave function has a nonzero amplitude to cross that barrier, i.e. from zero size to a small but definite size.
After the universe tunnelled into existence, Vilenkin’s model then incorporates inflation, a phase of rapid exponential expansion that occurred in the universe’s earliest moments.
In short, according to Vilenkin, the universe comes into being from a state of nothingness through quantum tunnelling. This process allows it to suddenly appear with a definite size, overcoming a classical barrier in a way that traditional physics can’t explain. Vilenkin’s theory contrasts with the Hartle-Hawking No Boundary proposal, which views time as finite but without a definite beginning or end, thus not pinpointing a specific commencement for the universe.
The elegance of this model is appealing, but I get stuck on his interpretation of “nothingness.” For most of us, “nothing” means a complete absence—no properties, no laws, no anything. But Vilenkin’s version of “nothing” includes pre-existing quantum laws. Quantum tunnelling only makes sense within a framework of rules, and if space-time only appears with the universe, where do those rules “live” before space-time exists? How could there be a pre-existing quantum field or set of rules before space-time existed? Vilenkin’s model leans on quantum rules that seem to ‘apply’ before spacetime comes into being, so in what sense can we still call that state ‘nothing’? Vilenkin’s model suggests that space-time emerges after the tunnelling event. So, which is it? If quantum laws and fields are already “there,” then something pre-universal exists, which undercuts the idea of a beginning from nothing.
Furthermore, Vilenkin’s “tunnelling wave function” calculates the probability of the universe jumping from a near-singular state to an expanding one through quantum tunnelling. This model describes how the nascent universe, facing a gravitational energy barrier, could overcome this barrier to facilitate expansion. What’s still murky to me, though, is that while Vilenkin’s model gives a clever mechanism for what happens after the real origin, it doesn’t actually explain emergence from literal “nothing”. The theory still invokes non-material, abstract mathematical laws that somehow exist prior to spacetime, matter, and energy—exactly the kind of transcendent reality that theism posits.
We’ve already asked whether the Hartle–Hawking model really explains the universe coming from “nothing.” The same issue shows up in Vilenkin’s approach. The complex mathematics in these theories assume some kind of pre-existing reality, albeit vaguely defined. Calling the starting point in these models “nothing” is misleading; this “nothing” is not an absolute void but a pre-geometric state that still has properties. So, when people say quantum principles allows creation from nothing, they’ve already smuggled “something” into the equation of “nothing.” This is a point of contention noted by philosopher of physics Willem B. Drees:
“Hawking and Hartle interpreted their wave function of the universe as giving the probability for the universe to appear from nothing. However, this is not a correct interpretation, since the normalisation presupposes a universe, not nothing.”[vi]
The notion of a universe with possible properties must first exist before quantum cosmologists can construct the universal wave function describing those properties as a superposition. Consider the double-slit experiment: when a photon hits the slits, we observe interference patterns that suggest superposition behaviour. The Schrödinger equation doesn’t tell us the photon “really” exists in multiple states; it tells us what detection patterns to expect given our experimental setup. The physical situation constrains what our mathematics can meaningfully describe. A similar logic applies to quantum cosmology. The Wheeler-DeWitt equation can generate a “wave function of the universe” with probabilities for different cosmic configurations, but this mathematical machinery presupposes a framework of possibilities it can work with. We’re not actually explaining the existence of the universe, we’re building tools that connect possible observations to predicted outcomes. Just as the photon must exist as a physical reality before QM can describe its interference patterns, a universe with potential properties must exist before the Wheeler-DeWitt equation can generate probability distributions over cosmic configurations.
This is why all these quantum cosmology models, no matter how sophisticated, seem to start with a universe already “in play” in some vague sense. A universe with certain possible properties precedes the mathematical procedures that produce a solution to the Wheeler-DeWitt equation—a universal wave function that assigns definite probabilities to the different possible attributes the universe could possess. So, while these models offer interesting insights into the universe’s developmental stages, they appear to start from a point where the universe, in some form, already exists.
Quantum cosmology is bewildering, and for good reason: it’s hard to picture what the math is really saying. We’re still very much in the “figuring it out” phase, so I think it’s best to treat bold claims and harsh critiques with healthy scepticism. I’ll admit my grasp is incomplete, though I think everyone’s is, and that’s part of exploring the unknown. The good news is that, in this section we’ll switch to firmer ground, focusing on philosophical ideas that I think are easier to follow.
In his work, “The Grand Design,” Stephen Hawking proposes a thought-provoking idea: “Because there is a law such as gravity, the universe can and will create itself from nothing. Spontaneous creation is the reason there is something rather than nothing, why the universe exists, why we exist. It is not necessary to invoke God to light the blue touch paper and set the universe going.” Similarly, Lawrence M. Krauss, drawing inspiration from Alexander Vilenkin’s work, argues that “The laws themselves require our universe to come into existence, to develop and evolve.”
When Hawking speaks of “a law such as gravity” being central to the universe’s creation, he’s referencing the entire mathematical edifice of quantum cosmology, including the universal wave function, the Wheeler-DeWitt equation, and modern theories of quantum gravity. The underlying assumption is that physical laws can do explanatory work that looks causal: they don’t just describe what happens; they help account for why anything happens at all, including a universe.
When scientists suggest that mathematical models can account for the existence of the universe, they might be unknowingly aligning with the ancient philosophies of Plato and Pythagoras. These thinkers wondered that if we can use mathematics to describe the effects of various phenomena, perhaps the underlying causes are mathematical too. So, can mathematical models actually cause physical phenomena?
Professor John Lennox makes an important point: we need to distinguish between causes and scientific laws. Causes refer to specific events that lead to other outcomes, whereas laws describe the general relationships between different events or variables. For example, gravity doesn’t “make” objects fall; it describes how mass and energy interact so that falling happens. This is because the laws of physics are interpretations of nature’s behaviour.
Think of simple arithmetic: 1 + 1 = 2. It’s true, but the formula doesn’t create anything. If I save $100 this month and $100 next month, the maths confirms I have $200. But if I don’t actually save, maths won’t grow my bank account. The claim that complex mathematical laws alone can conjure up the universe within a purely naturalistic frame borders on science fiction. In principle, theories and laws don’t have the creative power to explain the origin of matter, energy and spacetime. This is like saying that the lines of longitude and latitude on a map are responsible for the location of the Hawaiian Islands in the Pacific Ocean. While these laws may explain the universe’s structure and make its existence possible, it’s a completely different leap to suggest they’re responsible for creating it.
That’s why Stephen Hawking’s idea that “the law of gravity” explains “why there is something rather than nothing” reflects a deeper philosophical misunderstanding about the role and limits of physical laws. These laws, expressed in mathematical terms, are descriptive tools that explain how nature behaves and how its components interact, so even a “theory of everything” or the discovery of a new natural law wouldn’t bridge the gap between nothingness and the emergence of existence. No law of nature can do that job.
Consider the universal wave function. It outlines potential universes with varying gravitational fields. It describes the “superposition” of all conceivable universes, each with its own spatial geometry and mass-energy configuration. Intriguing, yes, but it doesn’t specify why any one universe should emerge from this spectrum of possibilities, or why anything should exist at all. In scenarios where spacetime, matter, and energy are absent, there is no physical mechanism within this framework to account for their sudden appearance.
In other words, these models do not provide a causal mechanism for the emergence of the universal wave function or the potential universes it describes. They describe what might be possible but fail to explain how or why these possibilities become real.
The Wheeler-DeWitt equation and the concept of curvature-matter pairings in superspace represent theoretical constructs or potential physical realities, but they remain, fundamentally, mathematical abstractions. The inherently theoretical nature of quantum cosmology, even when viewed as a foundational element of quantum gravity, does not pinpoint a physical cause for why the universe exists.
So, quantum cosmology excels at mapping out potential universes and their properties, but it struggles to explain why any particular universe materialised, or why there is something rather than nothing at all. Abstract mathematical models are great for describing physical phenomena but lack the creative power to actually generate a material reality. Mathematical entities describe; they do not cause. And if mathematical laws cannot create the universe, where, then, does their apparent explanatory power originate? Alexander Vilenkin wrestled with this and even floated the possibility of a “mind” behind it all:
“Does this mean that the laws are not mere descriptions of reality and can have an independent existence of their own? In the absence of space, time, and matter, what tablets could they be written upon? The laws are expressed in the form of mathematical equations. If the medium of mathematics is the mind, does this mean that mind should predate the universe?”[vii]
Many physicists agree that mathematical laws are simply descriptive tools—powerful frameworks that exist in the minds of physicists but lack generative power. Quantum cosmology thus suggests two possibilities: either mathematics somehow “creates” the universe (a position bordering on the mystical) or aligns with Mathematical Platonism, which claims that mathematical ideas exist in a non-physical realm.
I can see three ways to think about the relationship between the mathematics of quantum cosmology and the material universe:
- Mathematics is a post-universal mental phenomenon. It is merely a useful description of reality, which is not fundamentally mathematical.
- Mathematics exists prior to the universe in an abstract, immaterial realm independent of mind.
- Mathematics is a mental phenomenon and exists prior to the universe.
Among the three options, I believe the third makes the most sense based on our uniform experience. This is because:
- The world appears to fundamentally conform to mathematical principles independent of human minds, excluding the first conception. This conception would also rule out the idea under discussion—that mathematical laws cause the universe’s conception.
- There is no logical reason to believe the contents of an abstract realm independent of mind would be accessible to minds. As mathematics is accessible to our minds, this rules out the second conception.
- Mathematics is a mental phenomenon and the universe fundamentally conforms to mathematical principles, so this fits with the third conception.
If mathematical principles must have existed causally prior to the universe, yet mathematics is accessible to minds, not abstract from them, then doesn’t that imply a mind causally prior to the universe within which mathematical principles hold shape? Unlike a realm of disconnected mindless abstract mathematics, our minds can interact with mathematics because our minds are of the same kind as the mathematics generating Mind.
Of course, here we’re going well beyond the realms of empirical observation and scientific inquiry into deeply speculative philosophy. But the argument is that the concept of a transcendent Mind is a reasonable extension of the cosmological data, and provides a more logically robust explanation for the universe than abstract, mindless mathematics.
And to be clear, to say that mathematics is a mental phenomenon is not to say that we ‘invent’ mathematics. The proposal is that mathematical laws and principles exist independently of human minds, and that these were put in place by a transcendent Mind as part of the created order. Humans, through their intellectual capacities, discover these pre-existing truths. The ability of the human mind to understand and uncover mathematical truths reflects being made in the image of that transcendent Mind. This belief suggests a compatibility and connection between the human mind and the ‘divine’ mind.
The existence of a mind capable of conceiving complex mathematical concepts and the existence of a cosmos that operates on these principles are not coincidental, as it would be if mathematics pre-existed in an abstract, mindless realm. It makes sense to hold that this alignment points toward a universe that is a product of an intelligent mind, and that our minds are therefore somehow attuned (or attracted) to this underlying order.
We also have plenty of experience of ideas originating in the mental realm and, through deliberate effort, producing entities that embody those ideas. Even if matter and energy could emerge from “nothing,” the structured information that shapes the universe hints at some form of intelligence behind it. In that light, while general relativity points to a beginning, quantum cosmology leaves room for a conscious source behind it all.
If quantum cosmology points to a realm where mathematical concepts exist independently of our universe, it makes sense to think these ideas come from a higher mental source—a mind “above” the universe. This perspective resonates with Alexander Vilenkin’s thoughts, as he briefly considers a theistic interpretation of quantum cosmology, suggesting these mathematical ideas might reflect a higher intelligence.
Between Speculation and Certainty: Stephen Hawking’s Contributions and the Debate on Quantum Cosmology
Stephen Hawking was a titan of science and an inspiring symbol of the remarkable accomplishments someone with a disability can achieve. His pioneering work in the 1960s and 1970s set the stage for research areas that continue to flourish today. Hawking inspired millions, myself included, to delve into the mysteries of the universe. However, it is crucial to acknowledge his shortcomings, particularly those he failed to overcome. Like many brilliant scientific minds, Hawking was prone to becoming captivated by his own speculative ideas, discussing them with a certainty best reserved for well-established, robust theories.
Hawking’s no-boundary proposal, though speculative, was often presented with unyielding certainty. Concepts such as baby universes, a unifying theory of everything, and higher dimensions may be widespread, but they lack definitive evidence. Some aspects of these ideas remain untested, while others have failed to yield supporting evidence. Despite these shortcomings, Hawking championed them, much to the dismay of more cautious scientists. He seldom differentiated between validated theories and speculative ones, particularly when discussing his own conjectures. He portrayed his speculations as fact and made sweeping statements based on them.
Hawking, along with physicists like Laurence Krauss, sought to employ quantum cosmology as an alternative to the theistic implications of the Big Bang Theory and the cosmological singularity. They maintained that the mathematics behind solving the wave function demonstrated that our universe did not necessarily have a beginning and could have arisen from “nothing.” From this angle, Hawking claimed that quantum cosmology removed the need for a transcendent creator, presenting it as the ultimate scientific counter to the God hypothesis.
But this line of thinking has its problems. For instance, imagine if I told you I could build a house from nothing, but still requiring pre-existing building codes; an infinite Home Depot with all possible materials, and a first construction rule like “Start with door frames”. Have I truly created something from nothing? Or have I simply disguised the starting points by hiding them in the requirements? Hawking and James Hartle were able to solve the Wheeler-DeWitt wave equation for the universe by substituting imaginary time into the formula, resulting in a theoretical model of a universe akin to our own. Yet, it would also seem that their calculations inadvertently presuppose the existence of a universe (vaguely defined). Their calculations and results also required the intelligent selection of conditions compatible with a universe like ours. As a result, their work did not explain the existence of the universe from unaided nothing; it needed a pre-existent something, and it needed intelligence to add information and foresight. Additionally, mathematics is a mental phenomenon that appears to exist prior to the universe, suggesting the presence of a mind or intelligence that preceded the universe. Viewed this way, quantum cosmology doesn’t eliminate the need for a creator, and it doesn’t favour naturalism either; if anything, it can be read as lending more weight to the idea that intelligence preceded the universe.
[i] https://journals.aps.org/prd/abstract/10.1103/PhysRevD.28.2960
[ii] Hawking, S. A Brief History of Time: From the Big Bang to Black Holes (1988). London, UK: Bantam, 140-141.
[iii] A Brief History of Time, 136.
[iv] Vilenkin, A. “Quantum Cosmology”, 7.
[v] Hartle, J. “What Is Quantum Cosmology?” Closer to Truth. Retrieved from https://www.youtube.com/watch?v=s6wPcq5yb7s
[vi] https://link.springer.com/article/10.1007/BF00670817
[vii] Vilenkin, A. ‘Many Worlds in One’, 205.



